publications | Lucas Lestandi

2023

IJNME
An iterative multi-fidelity approach for model order reduction of multidimensional input parametric PDE systems

Manisha Chetry , Domenico Borzacchiello , Lucas Lestandi, and 1 more author

International Journal for Numerical Methods in Engineering, Jul 2023

Abs Bib DOI PDF

We propose a parametric sampling strategy for reduction of large scale PDE systems with multidimensional input parametric spaces by leveraging models of different fidelity. The design of this methodology allows a user to adaptively sample points ad hoc from a discrete training set with no prior requirement of error estimators. It is achieved by exploiting low-fidelity models throughout the parametric space to sample points using an efficient sampling strategy, and at the sampled parametric points, high-fidelity models are evaluated to recover the reduced basis functions. The low-fidelity models are then adapted with the reduced order models built by projection onto the subspace spanned by the recovered basis functions. The process continues until the low-fidelity model can represent the high-fidelity model adequately for all the parameters in the parametric space. Since the proposed methodology leverages the use of low-fidelity models to assimilate the solution database, it significantly reduces the computational cost in the offline stage. The highlight of this article is to present the construction of the initial low-fidelity model, and a sampling strategy based on the discrete empirical interpolation method. We test this approach on a 2D steady-state heat conduction problem for two different input parameters and make a qualitative comparison with the classical greedy reduced basis method and with random selection of points. Further, we test the efficacy of the proposed method on a 9-dimensional parametric non-coercive elliptic problem and analyze the computational performance based on different tuning of greedy selection of points.
@article{chetry_iterative_2023, title = {An iterative multi-fidelity approach for model order reduction of multidimensional input parametric {PDE} systems}, issn = {0029-5981}, journal = {International Journal for Numerical Methods in Engineering}, author = {Chetry, Manisha and Borzacchiello, Domenico and Lestandi, Lucas and Da Silva, Luisa Rocha}, month = jul, year = {2023}, }
Data-driven surrogate modelling of residual stresses in Laser Powder-Bed Fusion

Lucas Lestandi, Jian Cheng Wong , Guo Ying Dong , and 8 more authors

International Journal of Computer Integrated Manufacturing, Jul 2023

Publisher: Taylor and Francis Ltd.

Abs Bib DOI

In order to enable the industrialization of additive manufacturing, it is necessary to develop process simulation models that can rapidly predict part quality. Although multi-physics simulations have shown success at predicting residual stress, distortion, microstructure and mechanical properties of additively manufactured parts, they are generally too computationally expensive to be directly used in applications, such as optimization, controls, or digital twinning. In this study, a critical evaluation is made of how data-driven surrogate models can be used to model the residual stress of parts fabricated by Laser Powder-Bed Fusion. Residual stress data is generated by using an inherent-strain based process simulation for two families of part geometries. Three different models using varying levels of sophistication are compared: a multilayer perceptron (MLP), a convolutional neural network (CNN) based on the U-Net architecture, and an interpolation-based method based on mapping geometries onto a reference. All three methods were found to be sufficient for part design, providing mechanical predictions for a CPU time below 0.2 s, representing a runtime speed-up of at least 3900x. Neural network-based models are significantly more expensive to train compared to using interpolation. However, the generality of models based on the U-Net architecture is attractive for applications in optimization.
@article{lestandi_data-driven_2023, title = {Data-driven surrogate modelling of residual stresses in {Laser} {Powder}-{Bed} {Fusion}}, issn = {13623052}, journal = {International Journal of Computer Integrated Manufacturing}, author = {Lestandi, Lucas and Wong, Jian Cheng and Dong, Guo Ying and Kuehsamy, S. J. and Mikula, J. and Vastola, G. and Kizhakkinan, U. and Ford, C. S. and Rosen, D. W. and Dao, M. H. and Jhon, M. H.}, year = {2023}, note = {Publisher: Taylor and Francis Ltd.}, keywords = {additive manufacturing, radial basis functions, Laser Powder Bed Fusion, surrogate models, geometry parametrization, neural network}, google_scholar_id = {eQOLeE2rZwMC}, }

2022

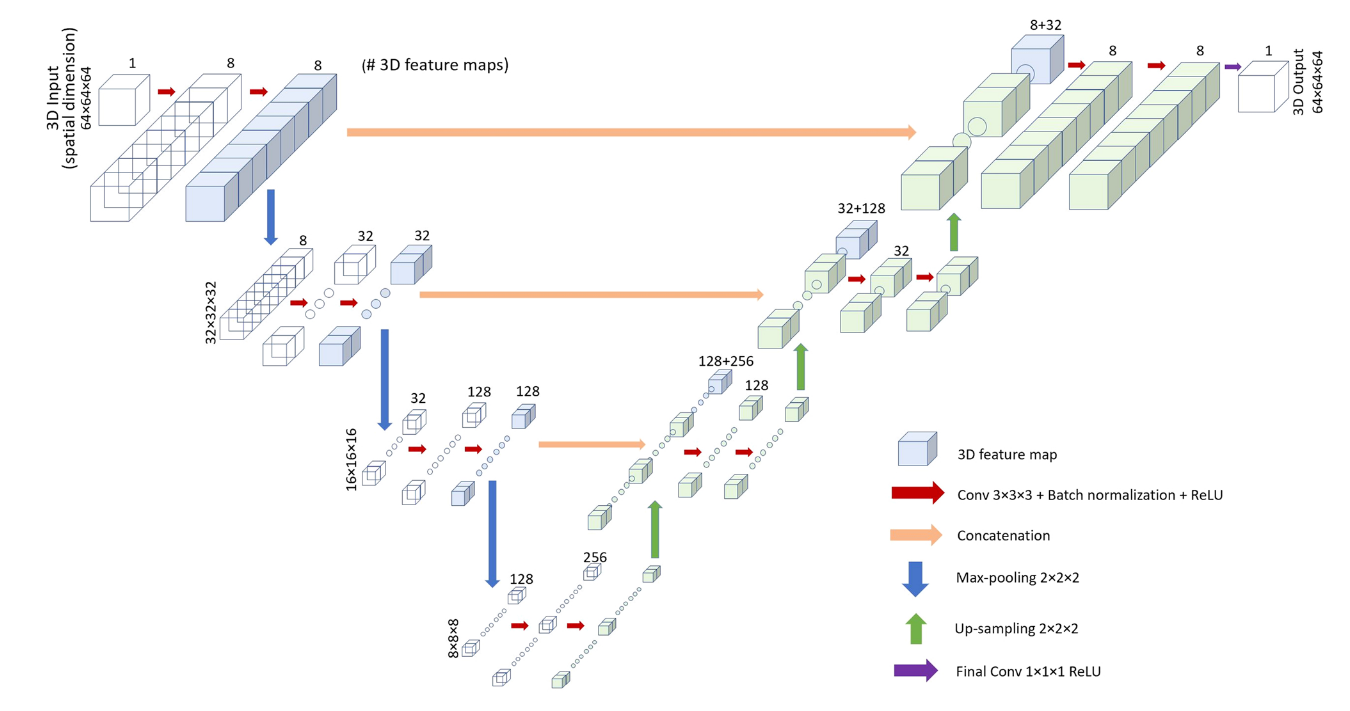A part-scale, feature-based surrogate model for residual stresses in the laser powder bed fusion process

Guoying Dong , Jian Cheng Wong , Lucas Lestandi, and 7 more authors

Journal of Materials Processing Technology, Jun 2022

Abs Bib DOI

Over the past decade, the Laser Powder Bed Fusion (LPBF) process has been widely used in the fabrication of industrial parts with advanced functions. It is known that the complex thermal processing of the material during the LPBF process has a significant influence on product quality. While high fidelity simulation models can account for the effects of processing, they are generally too computationally expensive to be directly used in the design of components. Consequently, in this paper we propose a surrogate model for Simulation Models of the residual stress at the part-scale based on a Convolutional Neural Network (CNN) with a 3D U-Net architecture. In order to model the wide range of geometries that can arise during the design process, we developed a feature-based approach in which we trained our CNN on combinations of three basic types of geometric features: circular struts, square struts, and walls. Data augmentation was utilized to account for orientation invariance. Several benchmarks were designed to test the performance of the surrogate model. Results demonstrated that a CNN with a 3D U-Net architecture can accurately predict the residual stress for the features designed. The average training and testing errors are 5.3% and 6.6%, respectively. Prediction performance for the benchmark parts led to validation errors of 14.4%− 28.3% due to their complex geometries. Nevertheless, this strategy led to a significant reduction in runtime, demonstrating that the proposed feature-based surrogate model has the potential to replace high fidelity process simulations for the design of practical engineering parts manufactured using LPBF.
@article{Dong2022, title = {A part-scale, feature-based surrogate model for residual stresses in the laser powder bed fusion process}, volume = {304}, issn = {09240136}, journal = {Journal of Materials Processing Technology}, author = {Dong, Guoying and Wong, Jian Cheng and Lestandi, Lucas and Mikula, Jakub and Vastola, Guglielmo and Jhon, Mark Hyunpong and Dao, My Ha and Kizhakkinan, Umesh and Ford, Clive Stanley and Rosen, David William}, month = jun, year = {2022}, keywords = {Additive manufacturing, Convolutional neural network, Powder bed fusion, Residual stress, Surrogate model}, pages = {117541}, }
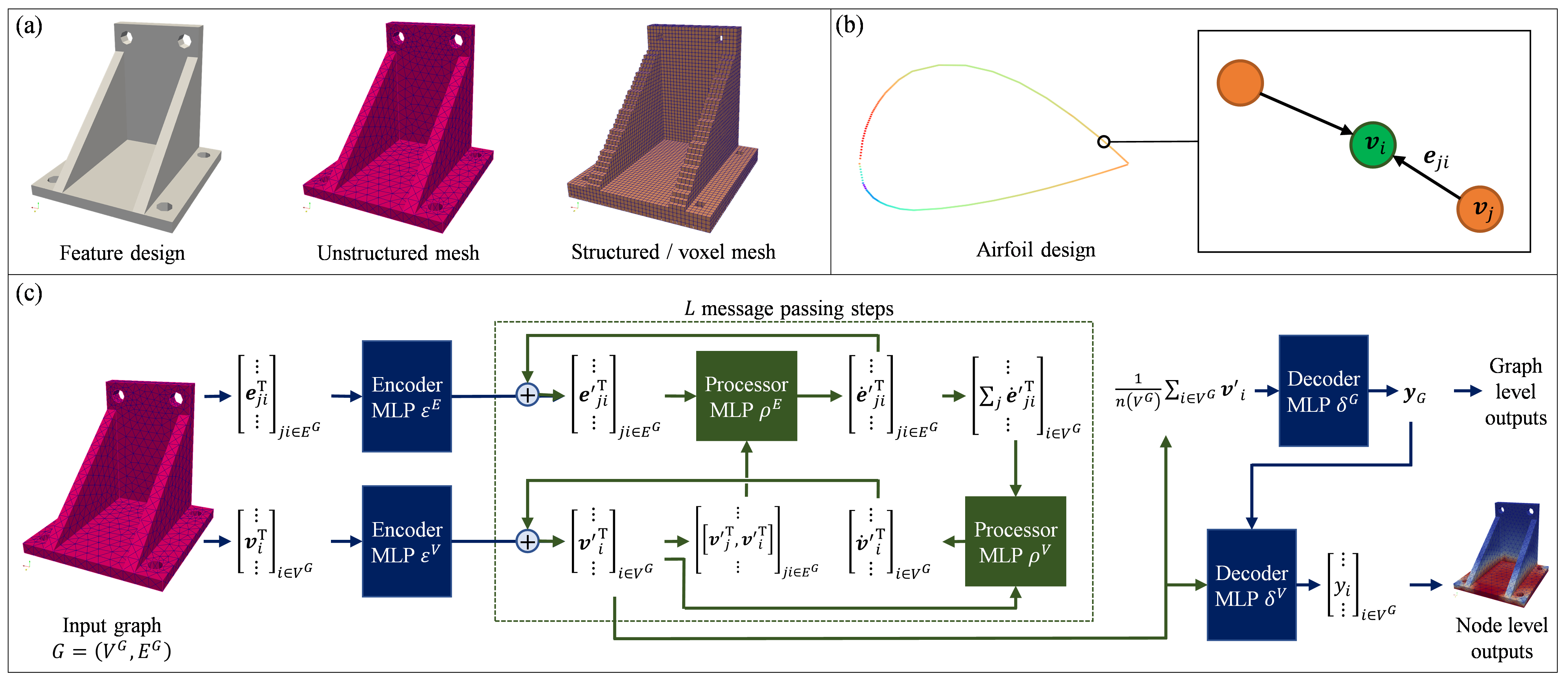Graph Neural Network Based Surrogate Model of PhysicsSimulations for Geometry Design

Jian Cheng Wong , Lucas Lestandi, David William Rosen , and 6 more authors

In 2022 IEEE Symposium Series on Computational Intelligence (SSCI) , Jun 2022

Abs Bib DOI PDF

Computational intelligent (CI) techniques have shown great potential as a surrogate model of expensive physics simulation, with demonstrated ability to make fast predictions, albeit at the expense of accuracy in some cases. For many scientific and engineering problems involving geometrical design, it is desirable for the surrogate models to precisely describe the change in geometry and predict the consequences. In that context, we develop graph neural networks (GNNs) as fast surrogate models for physics simulation, which allow us to directly train the models on 2/3D geometry designs that are represented by an unstructured mesh or point cloud, without the need for any explicit or hand-crafted parameterization. We utilize an encoder-processor-decoder-type architecture which can flexibly make prediction at both node level and graph level. The performance of our proposed GNN-based surrogate model is demonstrated on 2 example applications: feature designs in the domain of additive engineering and airfoil design in the domain of aerodynamics. The models show good accuracy in their predictions on a separate set of test geometries after training, with almost instant prediction speeds, as compared to O(hour) for the high-fidelity simulations required otherwise.
@inproceedings{wong_graph_2023, title = {Graph Neural Network Based Surrogate Model of PhysicsSimulations for Geometry Design}, author = {Wong, Jian Cheng and Lestandi, Lucas and Rosen, David William and Ooi, Chin Chun and Dong, Guoying and Jhon, Mark Hyunpong and Chattoraj, Joyjit and Kizhakkinan, Umesh and Dao, My Ha}, year = {2022}, booktitle = {2022 IEEE Symposium Series on Computational Intelligence (SSCI)}, pages = {1469-1475}, keywords = {Geometry;Training;Atmospheric modeling;Computational modeling;Predictive models;Graph neural networks;Task analysis;Graph neural network;fast surrogate model;physics simulation}, }

2021

JCP

Numerical Study of Low Rank Approximation Methods for Mechanics Data and Its Analysis

Lucas Lestandi

Journal of Scientific Computing, Apr 2021

Bib DOI

@article{Lestandi2021a,
  title = {Numerical {Study} of {Low} {Rank} {Approximation} {Methods} for {Mechanics} {Data} and {Its} {Analysis}},
  volume = {87},
  issn = {0885-7474},
  number = {1},
  journal = {Journal of Scientific Computing},
  author = {Lestandi, Lucas},
  month = apr,
  year = {2021},
  keywords = {Low rank approximation · tensor decomposition · HO},
  pages = {14},
}

2019

Chapter

Low Rank Approximation of Multidimensional Data In: Pirozzoli S., Sengupta T. (eds) High-Performance Computing of Big Data for Turbulence and Combustion.

Mejdi Azaïez , Lucas Lestandi, and Tomás Chacón Rebollo

In , Apr 2019

Bib DOI

@incollection{Azaiez2019,
  title = {Low {Rank} {Approximation} of {Multidimensional} {Data} {In}: {Pirozzoli} {S}., {Sengupta} {T}. (eds) {High}-{Performance} {Computing} of {Big} {Data} for {Turbulence} and {Combustion}.},
  volume = {592},
  isbn = {978-3-030-17011-0},
  publisher = {Springer International Publishing},
  author = {Azaïez, Mejdi and Lestandi, Lucas and Rebollo, Tomás Chacón},
  editor = {Sengupta, T.K. and Pirozzoli, S.},
  year = {2019},
  keywords = {POD, tensors, HOSVD, Data, Data reduction, Low rank approximation, Model Reduction, MOR, Singular Values Decomposition, Tensor train},
}

2018

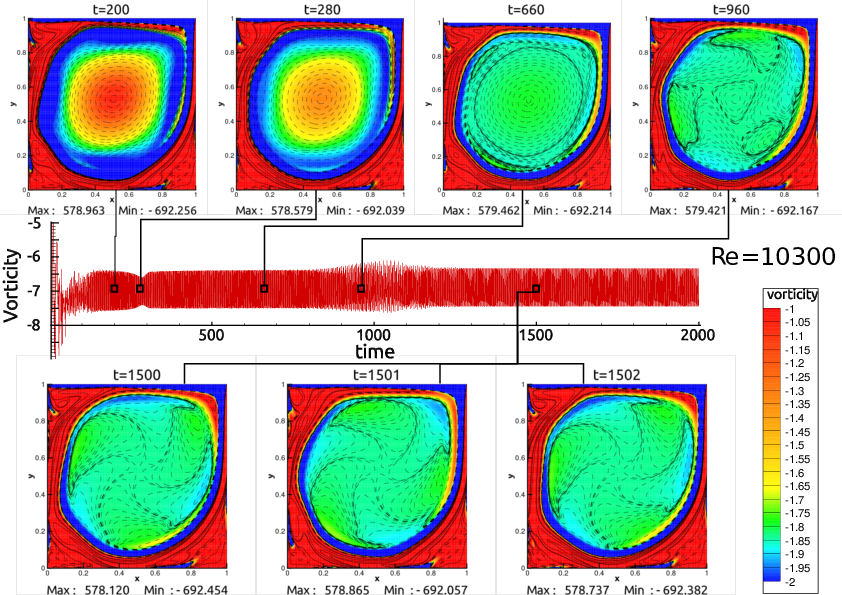Multiple Hopf bifurcations and flow dynamics inside a 2D singular lid driven cavity

Lucas Lestandi, Swagata Bhaumik , G. R. K. C. Avatar , and 2 more authors

Computers and Fluids, Apr 2018

Abs Bib DOI PDF

Two-dimensional (2D) flow inside a lid driven cavity (LDC) is shown to display multi-modal behavior in a consistent manner following the first Hopf bifurcation with varying Reynolds numbers (Re), depending upon the chosen spatial and temporal discretization scheme. Direct numerical simulation (DNS) following impulsive start, is used to show spatio-temporal growth and its nonlinear saturation of disturbance growth. Despite the fact that researchers have produced different value of Reynolds number when first Hopf bifurcation occurs (Recr1), DNS fundamentally differs from classical bifurcation studies involving global instability study of an equilibrium flow due to adopted nonlinear approach and not restricting the analysis to temporal instability only. The accuracy attribute of the DNS adopted here has been shown conclusively earlier via demonstration of a weak transient polygonal core vortex surrounded by relatively stronger gyrating vortices, which appear as a constellation after the disappearance of the transient, in [26]. Investigated LDC flow is characterized by multiple time scales at any Re, which are weak function of Re in selective intervals, punctuated by multiple bifurcations. The present investigation achieves two primary goals. First, it proposes to reconcile that Recr1 obtained by different numerical approaches can be shown to be in same range, provided the equilibrium flow obtained is of good quality, untainted by excessive diffusion. Secondly, we also show that for increasing Re following the first Hopf bifurcation, the flow during the limit cycle suffers a secondary instability, thus, requiring computation of the flow field over a longer time period. The first goal is met by exciting the flow field with a pulsating vortex inside the LDC for a very high accuracy scheme, we are able to show the universal nature of the primary bifurcation for Re in the range between 8020 and 8025. The flow at higher Re displays significantly increased spectral peaks, including broad-band spectrum and the understanding of all these have been aided by phase space portraits.
@article{Lestandi2018CF, title = {Multiple {Hopf} bifurcations and flow dynamics inside a {2D} singular lid driven cavity}, volume = {166}, issn = {0045-7930}, journal = {Computers and Fluids}, author = {Lestandi, Lucas and Bhaumik, Swagata and Avatar, G. R. K. C. and Azaiez, Mejdi and Sengupta, Tapan K.}, year = {2018}, keywords = {DNS, Lid driven cavity, Multiple Hopf bifurcation, po}, pages = {86-103}, google_scholar_id = {u5HHmVD_uO8C}, }
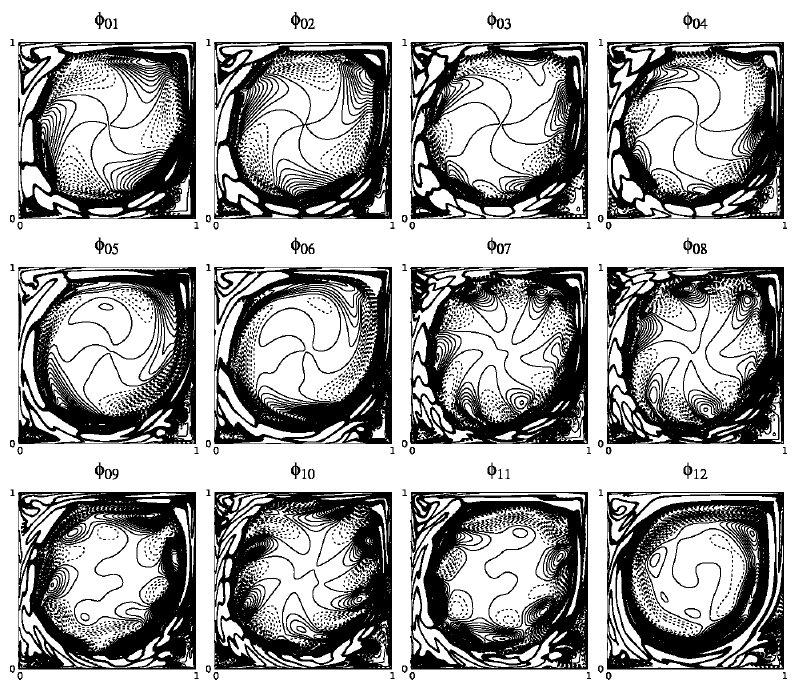POD Applied to Numerical Study of Unsteady Flow Inside Lid-driven Cavity

Lucas Lestandi, Swagata Bhaumik , Tapan K. Sengupta , and 2 more authors

Journal of Mathematical Study, Apr 2018

Abs Bib DOI

Flow inside a lid-driven cavity (LDC) is studied here to elucidate bifurcation sequences of the flow at super-critical Reynolds numbers (Recr1) with the help of analyzing the time series at most energetic points in the flow domain. The implication of Recr1 in the context of direct simulation of Navier-Stokes equation is presented here for LDC, with or without explicit excitation inside the LDC. This is aided further by performing detailed enstrophy-based proper orthogonal decomposition (POD) of the flow field. The flow has been computed by an accurate numerical method for two different uniform grids. POD of results of these two grids help us understand the receptivity aspects of the flow field, which give rise to the computed bifurcation sequences by understanding the similarity and differences of these two sets of computations. We show that POD modes help one understand the primary and secondary instabilities noted during the bifurcation sequences.
@article{Lestandi2018a, title = {{POD} {Applied} to {Numerical} {Study} of {Unsteady} {Flow} {Inside} {Lid}-driven {Cavity}}, volume = {51}, issn = {10066837}, number = {2}, journal = {Journal of Mathematical Study}, abrr = {JMS}, author = {Lestandi, Lucas and Bhaumik, Swagata and Sengupta, Tapan K. and Krishna Chand Avatar, G. R. and Azaïez, Mejdi}, year = {2018}, keywords = {dns, lid driven cavity, multiple hopf bifurcation, pod, pod modes analysis, polyg-}, pages = {150--176}, }
PhD Thesis
Low rank approximation techniques and reduced order modeling applied to some fluid dynamics problems

Lucas Lestandi

Université de Bordeaux , Apr 2018

Abs Bib DOI PDF

Numerical simulation has experienced tremendous improvements in the last decadesdriven by massive growth of computing power. Exascale computing has beenachieved this year and will allow solving ever more complex problems. But suchlarge systems produce colossal amounts of data which leads to its own difficulties.Moreover, many engineering problems such as multiphysics or optimisation andcontrol, require far more power that any computer architecture could achievewithin the current scientific computing paradigm. In this thesis, we proposeto shift the paradigm in order to break the curse of dimensionality byintroducing decomposition and building reduced order models (ROM) for complexfluid flows.This manuscript is organized into two parts. The first one proposes an extendedreview of data reduction techniques and intends to bridge between appliedmathematics community and the computational mechanics one. Thus, foundingbivariate separation is studied, including discussions on the equivalence ofproper orthogonal decomposition (POD, continuous framework) and singular valuedecomposition (SVD, discrete matrices). Then a wide review of tensor formats andtheir approximation is proposed. Such work has already been provided in theliterature but either on separate papers or into a purely applied mathematicsframework. Here, we offer to the data enthusiast scientist a comparison ofCanonical, Tucker, Hierarchical and Tensor train formats including theirapproximation algorithms. Their relative benefits are studied both theoreticallyand numerically thanks to the python library texttt{pydecomp} that wasdeveloped during this thesis. A …
@phdthesis{Lestandi2018, title = {Low rank approximation techniques and reduced order modeling applied to some fluid dynamics problems}, school = {Université de Bordeaux}, author = {Lestandi, Lucas}, year = {2018}, }
AMSES
Reduced order model of flows by time-scaling interpolation of DNS data

Tapan K Sengupta , Lucas Lestandi, S I Haider , and 2 more authors

Advanced Modeling and Simulation in Engineering Sciences, Oct 2018

Abs Bib DOI

A new reduced order model (ROM) is proposed here for reconstructing super-critical flow past circular cylinder and lid driven cavity using time-scaling of vorticity data directly. The present approach is a significant improvement over instability-mode (developed from POD modes) based approach implemented in Sengupta et al. [Phys Rev E 91(4):043303, 2015], where governing Stuart–Landau–Eckhaus equations are solved. In the present method, we propose a novel ROM that uses relation between Strouhal number (St) and Reynolds number (Re). We provide a step by step approach for this new ROM for any Re and is a general procedure with vorticity data requiring very limited storage as well as being extremely fast. We emphasize on the scientific aspects of developing ROM by taking data from close proximity of the target Re to produce DNS-quality reconstruction, while the applied aspect is also shown. All the donor points need not be immediate neighbors and the reconstructed solution has equivalent relaxed accuracy. However, one would restrain the range where the flow behavior is coherent between donors. The reported work is a proof of concept utilizing the external and internal flow examples, and this can be extended for other flows characterized by appropriate Re–St data.
@article{Sengupta2018, title = {Reduced order model of flows by time-scaling interpolation of {DNS} data}, volume = {5}, issn = {2213-7467}, number = {1}, journal = {Advanced Modeling and Simulation in Engineering Sciences}, author = {Sengupta, Tapan K and Lestandi, Lucas and Haider, S I and Gullapalli, Atchyut and Azaïez, Mejdi}, month = oct, year = {2018}, pages = {26}, }